Terry Jones

This is just a quick post. I have a ton of things I could say about this, but they’ll have to wait – I need to do some real work.

Last night and today I wrote some Python code to dig into the follower and following sets of Twitter users.

I also think I understand better why Twitter is so compelling, but that’s going to have to wait for now too.

You give my program some Twitter user names and it builds you a table showing numbers of followers, following etc. for each user. It distinguishes between people you follow and who don’t follow you, and people who follow you but whom you don’t follow back.

But the really interesting thing is to look at the intersection of some of these sets between users.

For example, if I follow X and they don’t follow me back, we can assume I have some interest in X. So if am later followed by Y and it turns out that X follows Y, I might be interested to know that. I might want to follow Y back just because I know it might bring me to the attention of X, who may then follow me. If I follow Y, I might want to publicly @ message him/her, hoping that he/she might @ message me back, and that X may see it and follow me.

Stuff like that. If you think that sort of thing isn’t important, or is too detailed or introspective, I’ll warrant you don’t know much about primate social studies. But more on that in another posting too.

As another example use, I plan to forward the mails Twitter sends me telling me someone new is following me into a variant of my program. It can examine the sets of interest and weight them. That can give me an automated recommendation of whether I should follow that person back – or just do the following for me.

There are lots of directions you could push this in, like considering who the person had @ talked to (and whether those people were followers or not) and the content of their Tweets (e.g., do they talk about things I’m interested or not interested in?).

Lots.

For now, here are links to a few sample runs. Apologies to the Twitter users I’ve picked on – you guys were on my screen or on my mind (following FOWA).

I’d love to turn these into nice Euler Diagrams but I didn’t find any decent open source package to produce them.

I’m also hoping someone else (or other people) will pick this up and run with it. I’ve got no time for it! I’m happy to send the source code to anyone who wants it. Just follow me on Twitter and ask for it.

Example 1: littleidea compared to sarawinge.
Example 2: swardley compared to voidspace.
Example 3: aweissman compared to johnborthwick.

And finally here’s the result for deWitt, on whose Twitter Python library I based my own code. This is the output you get from the program when you only give it one user to examine.

More soon, I guess.

Here’s a short summary of a failed experiment using the Principle of Inclusion/Exclusion to estimate how many users Twitter has. I.e., there’s no answer below, just the outline of some quick coding.

I was wondering about this over cereal this morning. I know some folks at Twitter, and I know some folks who have access to the full tweet database, so I could perhaps get that answer just by asking. But that wouldn’t be any fun, and I probably couldn’t blog about it.

I was at FOWA last week and it seemed that absolutely everyone was on Twitter. Plus, they were active users, not people who’d created an account and didn’t use it. If Twitter’s usage pattern looks anything like a Power Law as we might expect, there will be many, many inactive or dormant accounts for every one that’s moderately active.

BTW, I’m terrycojones on Twitter. Follow me please, I’m trying to catch Jason Calacanis.

You could have a crack at answering the question by looking at Twitter user id numbers via the API and trying to estimate how many users there are. I did play with that at one point at least with tweet ids, but although they increase there are large holes in the tweet id space. And approaches like that have to go through the Twitter API, which limits you to a mere 70 requests per hour – not enough for any serious (and quick) probing.

In any case, I was looking at the Twitter Find People page. Go to the Search tab and you can search for users.

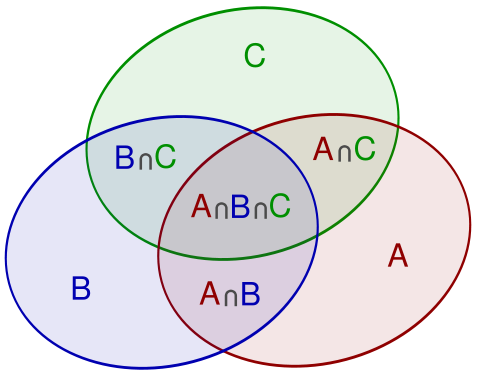
I searched for the single letter A, and got around 109K hits. That lead me to think that I could get a bound on Twitter’s size using the Principle of Inclusion/Exclusion (PIE). (If you don’t know what that is, don’t be intimidated by the math – it’s actually very simple, just consider the cases of counting the size of the union of 2 and 3 sets). The PIE is a beautiful and extremely useful tool in combinatorics and probability theory (some nice examples can be found in Chapter 3 of the introductory text Applied Combinatorics With Problem Solving). The image above comes from the Wikipedia page.

To get an idea of how many Twitter users there are, we can add the number of people with an A in their name to the number with a B in their name, …., to the number with a Z in their name.

That will give us an over-estimate though, as names typically have many letters in them. So we’ll be counting users multiple times in this simplistic sum. That’s where the PIE comes in. The basic idea is that you add the size of a bunch of sets, and then you subtract off the sizes of all the pairwise intersections. Then you add on the sizes of all the triple set intersections, and so on. If you keep going, you get the answer exactly. If you stop along the way you’ll have an upper or lower bound.

So I figured I could add the size of all the single-letter searches and then adjust that downwards using some simple estimates of letter co-occurrence.

That would definitely work.

But then the theory ran full into the reality of Twitter.

To begin with, Twitter gives zero results if you search for S or T. I have no idea why. It gives a result for all other (English) letters. My only theory was that Twitter had anticipated my effort and the missing S and T results were their way of saying Stop That!

Anyway, I put the values for the 24 letters that do work into a Python program and summed them:

count = dict(a = 108938,
             b =  12636,
             c =  13165,
             d =  21516,
             e =  14070,
             f =   5294,
             g =   8425,
             h =   7108,
             i = 160592,
             j =   9226,
             k =  12524,
             l =   8112,
             m =  51721,
             n =  11019,
             o =   9840,
             p =   8139,
             q =   1938,
             r =  10993,
             s =      0,
             t =      0,
             u =   8997,
             v =   4342,
             w =   6834,
             x =   8829,
             y =   8428,
             z =   3245)

upperBoundOnUsers = sum(count.values())
print 'Upper bound on number of users:', upperBoundOnUsers

The total was 515,931.

Remember that that’s a big over-estimate due to duplicate counting.

And unless I really do live in a tech bubble, I think that number is way too small – even without adjusting it using the PIE.

(If we were going to adjust it, we could try to estimate how often pairs of letters co-occur in Twitter user names. That would be difficult as user names are not like normal words. But we could try.)

Looking at the letter frequencies, I found them really strange. I wrote a tiny bit more code, using the English letter frequencies as given on Wikipedia to estimate how many hits I’d have gotten back on a normal set of words. If we assume Twitter user names have an average length of 7, we can print the expected numbers versus the actual numbers like this:

# From http://en.wikipedia.org/wiki/Letter_frequencies
freq = dict(a = 0.08167,
            b = 0.01492,
            c = 0.02782,
            d = 0.04253,
            e = 0.12702,
            f = 0.02228,
            g = 0.02015,
            h = 0.06094,
            i = 0.06966,
            j = 0.00153,
            k = 0.00772,
            l = 0.04025,
            m = 0.02406,
            n = 0.06749,
            o = 0.07507,
            p = 0.01929,
            q = 0.00095,
            r = 0.05987,
            s = 0.06327,
            t = 0.09056,
            u = 0.02758,
            v = 0.00978,
            w = 0.02360,
            x = 0.00150,
            y = 0.01974,
            z = 0.00074)

estimatedUserNameLen = 7

for L in sorted(count.keys()):
    probNotLetter = 1.0 - freq[L]
    probOneOrMore = 1.0 - probNotLetter ** estimatedUserNameLen
    expected = int(upperBoundOnUsers * probOneOrMore)
    print "%s: expected %6d, saw %6d." % (L, expected, count[L])

Which results in:

a: expected 231757, saw 108938.
b: expected  51531, saw  12636.
c: expected  92465, saw  13165.
d: expected 135331, saw  21516.
e: expected 316578, saw  14070.
f: expected  75281, saw   5294.
g: expected  68517, saw   8425.
h: expected 183696, saw   7108.
i: expected 204699, saw 160592.
j: expected   5500, saw   9226.
k: expected  27243, saw  12524.
l: expected 128942, saw   8112.
m: expected  80866, saw  51721.
n: expected 199582, saw  11019.
o: expected 217149, saw   9840.
p: expected  65761, saw   8139.
q: expected   3421, saw   1938.
r: expected 181037, saw  10993.
s: expected 189423, saw      0.
t: expected 250464, saw      0.
u: expected  91732, saw   8997.
v: expected  34301, saw   4342.
w: expected  79429, saw   6834.
x: expected   5392, saw   8829.
y: expected  67205, saw   8428.
z: expected   2666, saw   3245.

You can see there are wild differences here.

While it’s clearly not right to be multiplying the probability of one or more of each letter appearing in a name by the 515,931 figure (because that’s a major over-estimate), you might hope that the results would be more consistent and tell you how much of an over-estimate it was. But the results are all over the place.

I briefly considered writing some code to scrape the search results and calculate the co-occurrence frequencies (and the actual set of letters in user names). Then I noticed that the results don’t always add up. E.g., search for C and you’re told there are 13,190 results. But the results come 19 at a time and there are 660 pages of results (and 19 * 660 = 12,540, which is not 13,190).

At that point I decided not to trust Twitter’s results and to call it quits.

A promising direction (and blog post) had fizzled out. I was reminded of trying to use AltaVista to compute co-citation distances between web pages back in 1996. AltaVista was highly variable in its search results, which made it hard to do mathematics.

I’m blogging this as a way to stop thinking about this question and to see if someone else wants to push on it, or email me the answer. Doing the above only took about 10-15 mins. Blogging it took at least a couple of hours :-(

Finally, in case it’s not clear there are lots of assumptions in what I did. Some of them:

• We’re not considering non-English letters (or things like underscores, which are common) in user names.
• The mean length of Twitter user names is probably not 7.
• Twitter search returns user names that don’t contain the searched-for letter (instead, the letter appears in the user’s name, not the username).

I drove from Oakland up to the O’Reilly Foo camp last Friday. The O’Reilly offices are just outside Sebastopol, CA. I stopped at an ATM and my GPS unit got totally confused. So I took a few turns at random and wound up on Florence Avenue. I drove a couple of hundred meters and started seeing big colorful structures out the front of many houses. They were so good I stopped, got out my camera, and took a whole bunch of pictures.

I talked to a man washing his car in his driveway. He told me that “Patrick” had created all the figures, and installed them on the front lawns. I got the impression that it was all free. Soon after I found the house that was unmistakably Patrick’s and seeing a man loading things into a pickup truck I went up and asked if he was Patrick. It was him and we had a friendly talk (mainly me telling him he was amazing). He gave me a calendar of his work.

Click on the thumbnails below to see bigger versions. There’s even a FC Barcelona structure. As I found out later, lots of people (of course) have seen these sculptures. When I got to Foo, there was one (image above) outside the O’Reilly office. Google for Patrick Amiot or Florence Avenue, Sebastopol and you’ll find much more. And Patrick has his own web site.

In a belated attempt to educate myself by reading some of the things that many people study in high school, I’m reading The Histories of Herodotus. It’s highly entertaining and easy to read. I read The History of the Peloponnesian War by Thucydides a few years ago and enjoyed that even more. Herodotus is the more colorful, but the speeches and drama in Thucydides are fantastic.

There were lots of oracles in classical Greece, and elsewhere.Of the Greek oracles, the Delphic Oracle was, and still is, the best known. People (kings, dictators, emperors, wannabees) would send questions like “Should I invade Persia?” to the oracle and receive typically ambiguous or cryptic responses. We have a large number of famous oracular replies. Herodotus recounts how Croesus decided to test the various oracles by sending them all the same question, asking what he was doing on a certain day. The oracle at Delphi won hands down. Croesus then immediately put more pressing matters to the Delphic oracle, famously misinterpreted the pronouncements, and was duly wiped out by the Persians.

Imagine yourself in the position of the Delphic oracle. You’ve got all sorts of rulers and aspiring rulers constantly sending you their thoughts and questions, asking what you think. You’re in a unique position, simultaneously privy to the most secret potential plans of many powerful rulers. You really know what’s going on. You know what’s likely to succeed or to fail, and why. You get to give the thumbs up or thumbs down. By virtue of your position and the information flowing through your temple, you can direct traffic; you can shape and create history. You might even be tempted to profit from your knowledge. Your successful accurate pronouncements invariably reap you rich tribute.

OK, you can see where this is leading…

Sequoia Capital, and other well-known venture firms, have a somewhat similar position. They have thousands of leaders and wannabee leaders bringing them their detailed secret plans, proposing to mount armies, found cities, build empires, to attack the modern-day Persians, etc. By virtue of their unusual position they probably have a pretty good idea of what might work, and why. Using this knowledge, but without necessarily revealing sources, they can cryptically but assuredly state “oh, that’ll never work” or they can encourage ideas that are new and which they can see will somehow fit and succeed. If company X has consulted the oracle, disclosing a detailed plan to go left, and company Y plans to attack from the right, well…. why not?

Entrepreneurs beg an audience, get a tiny slice of time to make their pitch, and occasionally receive rare clear endorsements. Much more frequently they are left to scratch their heads over cryptic, ambiguous and unexplained responses (and non-responses). You can bet the Delphic oracle didn’t sign NDAs either.

It’s stretching it too far to seriously claim that Sequoia is the modern-day equivalent of the Delphic oracle. But on the other hand, over 2500 years have elapsed, so you’d expect a few changes.

I’ve spent a lot of time thinking about Twitter this year. Here are a few thoughts at random.

Obviously Twitter have tapped into something quite fundamental, which at a high level we might simply call human sociability. We humans are primates, though there’s a remarkably strong tendency to forget or ignore this. We know a lot about the intensely social lives of our fellow primate species. It shouldn’t come as a surprise that we like to Twitter amongst ourselves too.

Here are a couple of interesting (to me) reasons for the popularity of Twitter.

One is that many people are in some sense atomized by the fact that many of us now work in an isolated way. Technical people who can do their work and communicate over the internet probably see less of their peers than others do. That’s just a general point, it’s not specific to Twitter or to 2008. It would have seemed unfathomably odd to humans 50 years ago to hear that many of us would be doing a large percentage of our work and social communication via machines, interacting with people who we don’t otherwise know, and who we rarely or never meet face to face. The rise of internet-based communication is obviously(?) helping to fill a gap created by this generational change.

The second point is specific to Twitter. Through brilliance or accident, the form of communication on Twitter is really special. Building a social network on nothing-implied asymmetric follower relationships is not something I would have predicted as leading to success. Maybe it worked, or could have all gone wrong, just due to random chance. But I’m inclined to believe that there’s more to it than that. Perhaps we’re all secretly voyeurs, or stickybeaks (nosy-parkers). Perhaps we like to see one half of conversations and be able to follow along if we like. Perhaps there’s a small secret thrill to promiscuously following someone and seeing if they follow you back. I don’t know the answer, but as I said above I do think Twitter have tapped into something interesting and strong here. There’s a property of us, we simple primates, that the Twitter model has managed to latch onto.

I think Twitter should change the dynamics for new users by initially assigning them ten random followers. New users can easily follow others, but if no-one is following them….. why bother? New user uptake would be much higher if they didn’t have the (correct) feeling that they were for some reason expected to want to Twitter in a vacuum. You announce a new program, called e.g., Twitter Guides and ask for people to volunteer to be guides (i.e., followers) of newbees. Lend a hand, make new friends, maybe get some followers yourself, etc. Lots of people would click to be a Guide. I bet this would change Twitter’s adoption dynamics. If you study things like random graph theory and dynamic systems, you know that making small changes to (especially initial) probabilities can have a dramatic effect on overall structure. If Twitter is eventually to reach a mass audience (whatever that means), it should be an uncontestable assertion that anything which significantly reduces the difficulty for new users to get into using it is very important.

Twitter should probably fix their reliability issues sometime soon.

I say “probably” because reliability and scaling are obviously not the most important things. Twitter has great value. It must have, or it would have lost its users long ago.

There’s a positive side to Twitter’s unreliability. People are amazed that the site goes down so often. Twitter gets snarled up in ways that give rise to a wide variety of symptoms. The result seems to be more attention, to make the service somehow more charming. It’s like a bad movie that you remember long afterwards because it wasn’t good. We don’t take Twitter for granted and move on the next service to pop up – we’re all busy standing around making snide remarks, playing armchair engineer, knowing that we too might face some of these issues, and talking, talking, talking. Twitter is a fascinating sight. Great harm is done by its unreliability, but the fact that their success so completely flies in the face of conventional wisdom is fascinating – and the fact that we find it so interesting and compelling a spectacle is fantastic for Twitter. They can fix the scaling issues, I hope. They should prove temporary. But the human side of Twitter, its character as a site, the site we stuck with and rooted for when times were so tough, the amazing little site that dropped to the canvas umpteen times but always got back to its feet, etc…. All that is permanent. If Twitter make it, they’re going to be more than just a web service. The public outages are like a rock musician or movie star doing something outrageous or threatening suicide – capturing attention. We’re drawn to the spectacle and the drama. We can’t help ourselves: it is our selves. We love it, we hate it, it brings us together to gnash our teeth when it’s down. But do we leave? Change the channel? No way.

Twitter is both the temperamental child rock star we love and, often, the medium by which we discuss it – an enviable position!

I’m reminded of a trick I learned during tens of thousands of miles of hitch-hiking. A great place to try for a lift is on a fairly high-speed curve on the on-ramp to the freeway / motorway / autopista / autoroute etc. Stand somewhere where a speeding car can only just manage a stop and only just manage to pull in away from the following traffic. Conventional wisdom tells you that you’ll never get a ride. But the opposite is true – you’ll get a ride extremely quickly. Invariably, the first thing the driver says when you get in is “Why on earth where you standing there? You’re very lucky I managed to stop. No-one would have ever picked you up standing there!” I’ve done this dozens of times. Twitter—being incredibly, unbelievably, frustratingly, unreliable and running contrary to all received wisdom—is a powerful spectacle. Human psyche is a funny thing. That’s a part of why it’s probably impossible to foretell success when mass adoption is required.

If I were running Twitter, apart from working to get the service to be more reliable, I’d be telling the engineering team to log everything. There’s a ton of value in the data flowing into Twitter.

Just as Google took internet search to a new level by link analysis, there’s another level of value in Twitter that I don’t think has really begun to be tapped yet.

PageRank, at least as I understand its early operation, ran a kind of iterative relaxation algorithm assigning and passing on credit via linked pages. A similar thing is clearly possible with Twitter, and some people have commented on this or tried to build little things that assign some form of score to users. But I think there’s a lot more that can be done. Because the Twitter API isn’t that powerful (mainly because you’re largely limited to querying as a single authorized user) and certainly because it’s rate-limited to just 70 API calls an hour, this sort of analysis will need to be done by Twitter themselves. I’m sure they’re well aware of that. Rate limiting probably helps them stay up, but it also means that the truly interesting and valuable stuff can’t be done by outsiders. I have no beef with that – I just wish Twitter would hurry up and do some of it.

Some examples in no order:

• The followers to following ratio of a Twitter user is obviously a high-level measure of that user’s “importance” (in some Twitter sense of importance). But there’s more to it than that. Who are the followers? Who do they follow, who follows them? Etc. This leads immediately back to Google PageRank.
• If a user gets followed by many people and doesn’t follow those people back, what does it say about the people involved? If X follows Y and Y then goes to look at a few pages of X’s history but does not then follow X, what do we know?
• If X has 5K followers and re-tweets a twit of Y, how many of X’s followers go check out and perhaps follow Y? What kind of people are these? (How do you advertise to them, versus others?)
• Along the lines of co-citation analysis, Twitter could build up a map showing you who you might follow. I.e., you can get pairwise distances between users X and Y by considering how many people they follow in common and how many they follow not-in-common. That would lead to a people you should be following that you’re not kind of suggestion.
• Even without co-citation analysis (or similar), Twitter should be able to tell me about people that many of the people I follow are following but whom I am not following. I’d find that very useful.
• Twitter could tell me why someone chooses to follow me. What were they looking at (if anything) before they decided to follow me? I.e., were they browsing the following list of someone else? Did they see my user name mentioned in a Tweet? Did they come in from an outside link? Would a premium Twitter user pay to have that information?
• Twitter has tons of links. They know the news as it happens. They could easily create a news site like Digg.
• In some sense the long tail of Twitter is where the value is. For instance, it doesn’t mean much if a user following 10K others follows someone. But if someone is following just 10 people, it’s much more significant. There’s more information there (probably). The Twitter mega users are in some way uninteresting – the more people they have following them and the more they follow, the less you really know (or care) about them. Yes, you could probably figure out more if you really wanted to, but if someone has 10K followers all you really know is that they’re probably famous in some way. If they add another 100 followers it’s no big deal. (I say all this a bit lightly and generally – the details might of course be fascinating and revealing – e.g., if you notice Jason Calacanis and Dave Winer have suddenly started @ messaging each other again it’s like IRC coming back from a network split :-))
• Similarly if someone with a very high followers to following ratio follows a Twitter user who has just a couple of followers, it’s a safe bet that those two are somehow friends with a pre-existing relationship.
• I bet you could do a pretty good job of putting Twitter users into boxes just based on their overall behavior, something like the 16 Myers-Briggs categories. Do you follow people back when they follow you? Do you @ answer people who @ address you (and Twitter knows when you’ve seen the original message)? Do you send @ messages to people (and how influential are those people)? Do those people @ you back (and how influential those people are says something about how interesting / provocative you are)? Do you follow tons and tons of people? Do you follow people and then un-follow them if they don’t follow you back? Do you follow random links in other people’s Twitters, and are those links accompanied by descriptive text or tinyurl links? Do you @ message people after you follow their links? Do your Twitter times follow a strict pattern, or are you on at all hours, or suddenly spending days without Twittering? Do you visit and just read much more than you tweet? How much old stuff do you read? Do you tend to talk in public or via DM? Are your tweets public?All that without even considering the content of your Twitters.
• Could Twitter become a search engine? That’s not a 100% serious question, but it’s worth considering. I don’t mean just making the content of all tweet searchable, I mean it with some sort of ranking algorithm, again perhaps akin to PageRank. If you somehow rank results by the importance or closeness of the user whose tweets match the search terms, you might have something interesting.
• Twitter also presumably know who’s talking about whom in the DM backchat. They can’t use that information in obvious way, but it’s of high value.

I could go on for hours, but that’s more than enough for now. I don’t feel like any of the above list is particularly compelling, but I do think the list of nice things they could be doing is extremely long and that Twitter have only just begun (at least publicly) to tap into the value they’re sitting on.

I think Google should buy Twitter. They have what Twitter needs: 1) engineering and scale, 2) link analysis and algorithm brilliance, and 3) they’re in a position to monetize the value illustrated above (via their search engine, that already has ads) without pissing off the Twitter community by e.g., running ads on Twitter. What percentage of Twitter users also use Google? I bet it’s very high.

I’m a big fan of Google maps.

But sometimes they get things very very wrong. In January I posted this example of them getting the location of the San Francisco international airport way wrong.

The screenshot linked above is supposed to show the location of the hotel Princesa Sofia in Barcelona. They have the address right, the zip code looks about right, but the location is about 30 miles off.

Caveat turista.

I’ve been talking to people about raising money for Fluidinfo over the last 5 months. Along the way I’ve had plenty of time to reflect on the process. I have a series of blog posts saved up. They’re mainly about oddities and discrepancies between appearance and reality. I plan to write them up gradually. Here’s one I wrote earlier this year but which I never finished. It’s still unpolished – but what the hell. This is a blog, after all.

In September 2007, Fred Wilson posted asking whether VCs should blog. The first thing I thought about when I read his title was transparency.

Increased transparency is a side-effect of easier communication between people. There are many relatively opaque human institutions and professions that have persisted for decades or centuries, relying on the fact that their subjects or customers were unable to communicate easily, to self-organize, to be widely heard, etc. Exclusionary access to knowledge is the foundation of power. As barriers to communication begin to fall, openness and transparency increase. Cracks appear in the walls. At that point anything can happen. The typical response is a heavy-handed crackdown to maintain or regain control. Examples are so numerous and widespread that any small sample would be woefully inadequate. This never-ending dynamic is just a part of the human condition and the nature of power.

But in some arenas, especially when there’s a market or in repeated games (a rich area of game theory), there may be a competitive advantage to (usually) smaller players who act disruptively to deliberately increase transparency. Those players differentiate themselves by (often informally) defecting from the (often tacit) group of gatekeepers. Advantages may include potential clients tending to trust you more, wide attention, and better opportunities. If increased transparency gets a foothold, there can then follow a kind of race to the bottom as players reveal increasingly more formerly-inside knowledge. This is also a drama that has been played out many times, and it’s fascinating and educational to watch.

We’re now seeing the cracks open wide in the VC world. The rise of the VC blogger has provided us with hundreds of eye-holes through which we can get some view of the works. The VC bloggers are implicitly calling out their less open colleagues, challenging them to open up. An extreme example is Venture Hacks, written by VC industry insiders, whose aim is to “open source” VC strategy in order to aid entrepreneurs. Then there’s The Funded, which shook the VC world as formerly isolated entrepreneurs got together (and in relative privacy, no less!) to exchange opinions and experiences. While The Funded is unquestionably biased, and based on small sample sizes, part of the fuss was unquestionably about control.

I awoke yesterday with another thought about transparency, why VCs should blog, and the curious dynamics of the VC/entrepreneur dance.

VCs should also blog because it allows entrepreneurs to see who they are as people. That may sound trite, but I think it’s quite interesting.

I’ve attended probably 50 events where one or more VCs takes the stage and gives some kind of a presentation. The presentations are very often excruciatingly dull. That’s because they’re filled to bursting with VC clichés. Even when VCs make an effort to differentiate themselves they tend to use clichés! They’re active investors, they have deep experience, broad contacts, want to help management, etc. I sat in the audience at Le Web a couple of weeks ago while several investors were on stage doing their thing. I wound up laughing with the guy who sat next to me, who I’d never met before. We rolled eyes at each other, passed notes, and ended up whispering nasty and disrespectful comments during the presentation. We were obviously there because we were interested to learn more, but we were served up standard VC fare. Steak and eggs.

The interesting thing is that entrepreneurs are a wildly idiosyncratic bunch. One would therefore expect that they’d tend to highly appreciate signs of character and individuality in VCs. Meanwhile VCs tend to keep things buttoned down and insist on making dreary presentations.

If nothing else, the existing dynamics are amusing. Wild-eyed, power-hungry, idiosyncratic, unconventional, and often deeply weird entrepreneurs are trying to act straight, to project an image of reliability, stability, balance, good sense, etc., in order to get funded. Simultaneously, the VC companies the entrepreneurs are evaluating, and who partly rely on being attractive to entrepreneurs, go to lengths to homogenize themselves – in the process washing out the very thing that an entrepreneur might find most reassuring.

There’s opportunity in this discrepancy. VCs who blog about themselves, in addition to talking about their industry and flogging their portfolio companies, may have tapped into this. Allowing entrepreneurs to see what you’re like as a person is a differentiator.

I’ve only got so much time a day to read blogs, Twitters, etc.

With blogs I find that I tend to try to keep up with those that post at a frequency at or below what I can handle, irrespective of quality of content. There are lots of blogs that I really enjoy, but which post new material so often that I end up never going to their sites. E.g., BoingBoing or ReadWriteWeb. I tend to always go to new content at blogs I like that have about one new article a day. I have dozens of examples in both these categories.

With blogs it’s no problem if some of the sites you’re subscribed to have tons of content. If you never click through on the indicator that there are 500 unread postings, you never see them.

On Twitter though the dynamic is very different. I follow about 140 people. From time to time during the day – normally when I’m drinking a coffee like I am now, or eating food – I’ll go have a look at Twitter to see what’s up in the wider world.

Unlike with blogs, if someone posts hundreds of Twitter updates you’re going to see them all. You’re perhaps going to see something like the image above (click for larger version). That’s not what I want to see at all. I’m hoping to see a whole bunch of people posting a few things, not screen after screen of one person talking to many people I don’t know or follow. It’s worse than being in a room with someone talking loudly on a mobile phone, hearing just one side of the conversation – this is like being in a room with that same person, but they’re talking to multiple people at once.

So with some reluctance I have recently un-followed Scobelizer, guykawasaki and cameronreilly. I actually like much of their content, but they have much too much of an unbalancing effect on my overall Twitter experience.

Move along.

Back in November I wrote some comments on Mahalo in an article titled The Mahalo-Wikipedia-Google love triangle.

I just read Jason‘s comment that they’re staying up late to make a Mahalo page on the Super Smash Bros Brawl Walkthrough.

That’s interesting.

Mahalo is supposed to be making things so easy that our grandparents can use it. But my grandparents are all dead, and they certainly wouldn’t be playing Super Smash Bros Brawl if they were alive.

Thinking about this, I was struck by another thought.

Who’s this page for? Why stay up til after midnight to buy and play a kids’ game and document it on Mahalo? Couldn’t it wait? What are those guys smoking up there in LA?

Then the penny dropped. Another penny. If you’re the first site on the web that’s got the Super Smash Bros Brawl walkthrough, kids are going to go to your page first thing tomorrow. And they’re not just going to your page, they’re going to Mahalo.

They’re also going to link to your page, and we all know what that means.

Meanwhile, the latte-sipping crowd who like the feel of Wikipedia being an online encyclopedia can look down their noses and have joint editing catfights over just what should be on the Wikipedia page.

If Mahalo keep it up, might they not look like the default cool destination for baby-chino-sipping teens and pre-teens to go to to find things about their popular culture? Just like you and I head to Wikipedia to look things up, might not kids make Mahalo their destination of choice to find current cultural stuff? Might not Wikipedia look to them as slow-moving, quaint and, dare I say it, even out of date as a print encyclopedia now looks to us grown ups?

I think I’m very slow on the uptake on this one. But I don’t spend much time thinking about Mahalo, so perhaps I can be excused. My kids are into Webkinz and of course there’s Webkinz stuff in Mahalo. My grandparents aren’t into that either.

Jason’s point, that Mahalo isn’t designed for geeks like us, is well taken. But I’ve only heard examples of how older folks want a simplified and more guided experience. Going for teens and pre-teens would be nice too. It might even be worth staying up after midnight for.

Obvious in retrospect, I guess, but I was slow to see it.

I have about ten things I could blog about today. Hopefully I wont.

I think I’m going to go out and make an impulse purchase a bit later. Can something be an impulse purchase if you blog about it first? I was in an Office Depot store today. Digital cameras are so cheap it’s ridiculous. Then throw in the value of the euro. For $129 I could pick up a 7M pixel Casio Exilim with a 3 inch screen. Why not? My old camera is a bit of a joke. Or there are nice Canon digital Elph cameras for $150. It’s hardly worth thinking about whether to buy one.

I’m getting glasses. Again. I had Lasik surgery in 2002 or so, and it’s been a wonderful 6 years. But my eyes are getting worse. I hated trying on glasses in the store today. I’ll hardly ever wear them I guess, but it’s clear (fuzzy?) to me that I’d be much better off with them.

I like women. They’re so much more interesting than men, not to mention a few other adjectives. I have a whole blog post on that one, but I’ll probably refrain.

I have two related postings: a book I’ll never write, and a Twitter  app I’ll never build. I should write them down. Twitter has so much interesting and valuable information in it. I wish their API was richer so that more things could be built. I hope they’re building some of them.

I still don’t understand why it’s considered valuable to have an API that many people build on, killing your service, if it can’t be easily monetized.

I’m booking yet another US trip. I went Silver on Delta in just 2 months this year, and am about to go Gold. This could be a Platinum year. BUT, I have to stop traveling and plant my ass on my chair in Barcelona and write more code. Have to. Must stop talking.

John Cleese’s speech at Graham Chapman’s funeral service is so moving. Can someone please do that for me?

Here’s a great example of terrible (for me at least) UI design.

I was just trying to change a ticket booking at Cheaptickets. Here’s the interface for selecting what you want to change (click to see the full image).

As you can see, I indicated a date/time change on my return flight. When I clicked on the continue button, I got an error message:

An error has occurred while processing this page. Please see detail below. (Message 1500)

Please select flight attributes to change.

I thought there was some problem with Firefox not sending the information that I’d checked. So I tried again. Then I tried clicking a couple of the boxes. Then I tried with Opera. Then I changed machines and tried with IE on a windows box. All of these got me the exact same error.

I looked at the page several times to see if I’d missed something – like a check box to indicate which of the flights to change. I figured Cheaptickets must have an error server side. Then I thought come on, you must be doing something wrong.

Then I figured it out. Can you?

I seem to be done with Twitter, at least for now. The graphic shows my monthly usage graph (courtesy of tweetstats) – click for the full-sized image.

I do find Twitter valuable, but I don’t want to spend time on it. It’s a bit like TV or video games for me – I quite enjoy those things, but there are almost always better things to do.

I’ll probably subscribe to some form of Twitter alert or digest at some point. I do find it useful to know when people are coming to Barcelona. But I don’t want to monitor Twitter. Like IM, I find it too distracting and waste too much time just going to check if anything’s new.

Etc.

I spent last weekend at the Open Social Foo camp held on the O’Reilly campus in Sebastopol, CA. The camp was organized by David Recordon and Scott Kveton, with sponsorship from various companies, especially including O’Reilly. I was lucky enough to have my airfare paid for, so lots of thanks to all concerned for that.

The camp was great. Very few people actually camped, almost everyone just found somewhere to sleep in the O’Reilly offices. Many of us didn’t sleep that much anyway.

There’s something about the modern virtual lifestyle that so many of us lead that leaves a real social hole. It’s been about 20 years since I really hung out at all hours with other coders. It’s something I associate most strongly with being an undergrad, with working at Micro Forté, and then in doing a lot of hacking as a grad student at The University of Waterloo in Canada.

So even though it was just 48 hours at the foo camp, it was really great. It’s not often I have the pleasurable feeling of being surrounded by tons of people who know way way more than I do about almost everything under discussion. That’s not meant to sound arrogant – I mean that I don’t get out enough, and I don’t live in SF, etc. It’s nice to have spent many years hanging around universities studying all sorts of relatively obscure and academic topics, and sometimes you wonder what everyone else was doing. Some of those people spent the years hacking really deeply on systems, and their knowledge appears encyclopedic next to the smattering of stuff I picked up along the way. It’s nice to bump into a whole bunch of them at once. It was extremely hard to get a word in in many of the animated conversations, which reminded me at times of discussions at the Santa Fe Institute. That’s a bit of a pain, but it’s still far better than some alternatives – e.g., not having a room full of super confident deeply knowledgeable people who all want to have their say, even if that means trampling all over others, ignoring what the previous speaker said, not leaving even 1/10th of a second conversational gap, and just plain old bull-dozering on while others try to jump in and wrest away control of the conversation.

I could write much more about all this.

I also played werewolf with up to 20 others on the Saturday night. In some ways I don’t really like the game, but it’s fun to sit around with a bunch of smart people of all ages who are all trying to convince each other they’re telling the truth when you know for sure some are lying. I was up until 4:30am that night. I went to the office I slept in on the Friday night, but found it had about 10 people still up, all talking about code. When I got up at 8am the next morning, they were all still there, still talking about code. I felt a bit guilty, like a glutton, for allowing myself three and a half hours sleep. Nice.

OK…. I should have realized in my original posting that the Oct 2007 10,000,000,000,000 objects figure was the source of the problem. I knew S3 could not be doubling every week, and that Amazon could not be making $11B a month, but didn’t see the now-obvious error in the input.

So what sort of money are they actually making?

Don MacAskill pointed me to this article at Forbes which says the number of objects at the end of 2007 was up to 14B from 10B in October. So let’s suppose the number now stands at 15B (1.5e10) and that Amazon are currently adding about 1B objects a month.

I’ll leave the other assumptions alone, for now.

Amazon’s S3 pricing for storage is $0.15 per GB per month. Assume all this data is stored on their cheaper US servers and that objects take on average 1K bytes. So that’s roughly 1.5e10 * 1e3 / 1e9 = 1.5e4 gigabytes in storage, for which Amazon charges $0.15 per month, or $2250.

Next, let’s do incoming data transfer cost, at $0.10 per GB. That’s simply 2/3rds of the data storage charge, so we add another 2/3 * $2250, or $1500.

Then the PUT requests that transmit the new objects: 1B new objects were added in the last month. Each of those takes a PUT, and these are charged at $0.01 per thousand, so that’s 1e9 / 1e3 * $0.01, or $10,000.

Lastly, some of the stored data is being retrieved. Some will just be backups, and never touched, and some will simply not be looked at in a given month. Let’s assume that just 1% of all (i.e., not just the new) objects and data are retrieved in any given month.

That’s 1.5e10 * 1e3 * 0.01 / 1e9 = 150 GB of outgoing data, or 0.15K TB. That’s much less than 10TB, so all this goes out at the highest rate, $0.18 per GB, giving another $27 in revenue.

And if 1% of objects are being pulled back, that’s 1.5e10 * 0.01 = 1.5e8 GET operations, which are charged at $0.01 per 10K. So that’s 1.5e8 / 1e4 * $0.01 = $150 for the GETs.

This gives a total of $2250 + $1500 + $10,000 + $27 + $150 = $13,927 in the last month.

And that doesn’t look at all like $11B!

Where did all that revenue go? Mainly it’s not there because Amazon only added 1e9 objects in the last month, not 1e15. That’s six orders of magnitude. So instead of $11B in PUT charges, they make a mere $11K. That’s about enough to pay one programmer.

I created a simple Amazon S3 Model spreadsheet where you can play with the numbers. The cells with the orange background are the variables you can change in the model. The variables we don’t have a good grip on are the average size of objects and the percentage of objects retrieved each month. If you increase average object size to 1MB, revenue jumps to $3.7M.

BTW, the spreadsheet has a simplification: regarding all data as being owned by one user, and using that to calculate download cost. In reality there are many users, and most of them will be paying for all their download data at the top rate. Also note that my % of objects retrieved is a simplification. Better would be to estimate how many objects are retrieved (i.e., including objects being retrieved multiple times) as well as estimating the download data amount. I roll these both into one number.

Before leaving Barcelona yesterday morning, I checked Google maps to get driving directions from San Francisco International airport (SFO) to a friend’s place in Oakland.

Google got it way wrong. Imagine trying to follow these instructions if you didn’t know they were so wrong. Click on the image to see the full sized map. Google maps is working again now.

Note: this posting is based on an incorrect number from an Amazon slide. I’ve now re-done the revenue numbers.

We’ve been playing around with Amazon’s Simple Storage Service (S3).

Adam Selipsky, Amazon VP of Web Services, has put some S3 usage numbers online (see slides 7 and 8). Here are some numbers on those numbers.

There were 5,000,000,000 (5e9) objects inside S3 in April 2007 and 10,000,000,000,000 (1e13) in October 2007. That means that in October 2007, S3 contained 2,000 times more objects than it did in April 2007. That’s a 26 week period, or 182 days. 2,000 is roughly 2¹¹. That means that S3 is doubling its number of objects roughly once every 182/11 = 16.5 days. (That’s supposing that the growth is merely exponential – i.e., that the logarithm of the number of objects is increasing linearly. It could actually be super-exponential, but let’s just pretend it’s only exponential.)

First of all, that’s simply amazing.

It’s now 119 days since the beginning of October 2007, so we might imagine that S3 now has 2^119/16.5 or about 150 times as many objects in it. That’s 1,500,000,000,000,000 (1.5e15) objects. BTW, I assume by object they mean a key/value pair in a bucket (these are put into and retrieved from S3 using HTTP PUT and GET requests).

Amazon’s S3 pricing for storage is $0.15 per GB per month. Assume all this data is stored on their cheaper US servers and that objects take on average 1K bytes. These seem reasonable assumptions. (A year ago at ETech, SmugMug CEO Don MacAskill said they had 200TB of image data in S3, and images obviously occupy far more than 1K each. So do backups.) So that’s roughly 1.5e15 * 1K / 1G = 1.5e9 gigabytes in storage, for which Amazon charges $0.15 per month, or $225M.

That’s $225M in revenue per month just for storage. And growing rapidly – S3 is doubling its number of objects every 2 weeks, so the increase in storage might be similar.

Next, let’s do incoming data transfer cost, at $0.10 per GB. That’s simply 2/3rds of the data storage charge, so we add another 2/3 * $225M, or $150M.

What about the PUT requests, that transmit the new objects?

If you’re doubling every 2 weeks, then in the last month you’ve doubled twice. So that means that a month ago S3 would have had 1.5e15 / 4 = 3.75e14 objects. That means 1.125e15 new objects were added in the last month! Each of those takes an HTTP PUT request. PUTs are charged at one penny per thousand, so that’s 1.125e15 / 1000 * $0.01.

Correct me if I’m wrong, but that looks like $11,250,000,000.

To paraphrase a scene I loved in Blazing Saddles (I was only 11, so give me a break), that’s a shitload of pennies.

Lastly, some of that stored data is being retrieved. Some will just be backups, and never touched, and some will simply not be looked at in a given month. Let’s assume that just 1% of all (i.e., not just the new) objects and data are retrieved in any given month.

That’s 1.5e15 * 1K * 1% / 1e9 = 15M GB of outgoing data, or 15K TB. Let’s assume this all goes out at the lowest rate, $0.13 per GB, giving another $2M in revenue.

And if 1% of objects are being pulled back, that’s 1.5e15 * 1% = 1.5e13 GET operations, which are charged at $0.01 per 10K. So that’s 1.5e13 / 10K * $0.01 = $15M for the GETs.

This gives a total of $225M + $150M + $11,250M + $2M + $15M = $11,642M in the last month. That’s $11.6 billion. Not a bad month.

Can this simple analysis possibly be right?

It’s pretty clear that Amazon are not making $11B per month from S3. So what gives?

One hint that they’re not making that much money comes from slide 8 of the Selipsky presentation. That tells us that in October 2007, S3 was making 27,601 transactions per second. That’s about 7e10 per month. If Amazon was already doubling every two weeks by that stage, then 3/4s of their 1e13 S3 objects would have been new that month. That’s 7.5e12, which is 100 times more transactions just for the incoming PUTs (no outgoing) than are represented by the 27,601 number. (It’s not clear what they mean by transaction – I mean what goes on in a single transaction.)

So something definitely doesn’t add up there. It may be more accurate to divide the revenue due to PUTs by 100, bringing it down to a measly $110M.

An unmentioned assumption above is that Amazon is actually charging everyone, including themselves, for the use of S3. They might have special deals with other companies, or they might be using S3 themselves to store tons of tiny objects. I.e., we don’t know that the reported number is of paid objects.

There’s something of a give away the razors and charge for the blades feel to this. When you first see Amazon’s pricing, it looks extremely cheap. You can buy external disk space for, e.g., $100 for 500GB, or $0.20 per GB. Amazon charges you just $0.18 per GB for replicated storage. But that’s per month. A disk might last you two years, so we could conclude that Amazon is e.g., 8 or 12 times more expensive, depending on the degree of replication. But you don’t need a data center or to grow (or shrink) a data center, cooling, employees, replacement disks—all of which have been noted many times—so the cost perhaps isn’t that high.

But…. look at those PUT requests! If an object is 1K (as above), it takes 500M of them to fill a 500GB disk. Amazon charges you $0.01 per 1000, so that’s 500K * $0.01 or $5000. That’s $10 per GB just to access your disk (i.e., before you even think about transfer costs and latency), which is about 50 times the cost of disk space above.

In paying by the PUT and GET, S3 users are in effect paying Amazon for the compute resources needed to store and retrieve their objects. If we estimate it taking 10ms for Amazon to process a PUT, then 1000 takes 10 seconds of compute time, for which Amazon charges $0.01. That’s nearly $26K per month being paid for machines to do PUT storage, which is 370 times more expensive than what Amazon would charge you to run a small EC2 instance for a month. Such a machine probably costs Amazon around $1500 to bring into service. So there’s no doubt they’re raking it in on the PUT charges. That makes the 5% margins of their retailing operation look quaint. Wall Street might soon be urging Bezos to get out of the retailing business.

Given that PUTs are so expensive, you can expect to see people encoding lots of data into single S3 objects, transmitting them all at once (one PUT), and decoding when they get the object back. That pushes programmers towards using more complex formats for their data. That’s a bad side-effect. A storage system shouldn’t encourage that sort of thing in programmers.

Nothing can double every two weeks for very long, so that kind of growth simply cannot continue. It may have leveled out in October 2007, which would make my numbers off by roughly 2^119/16.5 or about 150, as above.

When we were kids they told us that the universe has about 2⁸⁰ particles in it. 1.5e15 is already about 2⁵⁰, so only 30 more doubling are needed, which would take Amazon just over a year. At that point, even if all their storage were in 1TB drives and objects were somehow stored in just 1 byte each, they’d still need about 2⁴⁰ disk drives. The earth has a surface area of 510,065,600 km² so that would mean over 2000 Amazon disk drives in each square kilometer on earth. That’s clearly not going to happen.

It’s also worth bearing in mind that Amazon claims data stored into S3 is replicated. Even if the replication factor is only 2, that’s another doubling of the storage requirement.

At what point does this growth stop?

Amazon has its Q4 2007 earnings call this Wednesday. That should be revealing. If I had any money I’d consider buying stock ASAP.

I’ve had it with Mac OS X.

I’m going to install Linux on my MacBook Pro laptop in March once I’m back from ETech.

I’ve been thinking about this for months. There are just so many things I don’t like about Mac OS X.

Yes, it’s beautiful, and there are certainly things I do like (e.g., iCal). But I don’t like:

• Waiting forever when I do a rm on a big tree
• Sitting wondering what’s going on when I go back to a Terminal window and it’s unresponsive for 15 seconds
• Weird stuff like this
• Case insensitive file names (see above problem)
• Having applications often freeze and crash. E.g. emacs, which basically never crashes under Linux

I could go on. I will go on.

I don’t like it when the machine freezes, and that happens too often with Mac OS X. I used Linux for years and almost never had a machine lock up on me. With Mac OS X I find myself doing a hard reset about once a month. That’s way too flaky for my liking.

Plus, I do not agree to trade a snappy OS experience for eye candy. I’ll take both if I can have them, but if it’s a choice then I’ll go back to X windows and Linux desktops and fonts and printer problems and so on – all of which are probably even better than they already were a few years back.

This machine froze on me 2 days ago and I thought “Right. That’s it.” When I rebooted, it was in a weird magnifying glass mode, in which the desktop was slightly magnified and moved around disconcertingly whenever I moved the mouse. Rebooting didn’t help. Estéve correctly suggested that I somehow had magnification on. But, how? WTF is going on?

And, I am not a fan of Apple.

In just the last two days, we have news that 1. Apple crippled its DTrace port so you can’t trace iTunes, and 2. Apple QuickTime DRM Disables Video Editing Apps so that Adobe’s After Effects video editing software no longer works after a QuickTime update.

It’s one thing to use UNIX, which I have loved for over 25 years, but it’s another thing completely to be in the hands of a vendor who (regularly) does things like this while “upgrading” other components of your system.

Who wants to put up with that shit?

And don’t even get me started on the iPhone, which is a lovely and groundbreaking device, but one that I would never ever buy due to Apple’s actions.

I’m out of here.

I just deactivated my Facebook account. This has nothing to do with Robert Scoble’s account being disabled earlier today, I’m just sick of Facebook. It does nothing whatsoever for me, except send messages that can and would otherwise have been sent in email. I don’t want to use a tool that encourages people to send me messages on a website that I then have to go log in to. I don’t want some website to hold my messages. I like them to be searchable with things like grep. I like to organize them my way. I like email. Apart from receiving messages in a totally unattractive way, Facebook is useless for me – just a steady stream of invitations to things I don’t want to attend from people I don’t know, plus a smattering of cream pies, flying sheep, etc. So I’m outta there. I wonder if I’ll manage to survive.

I’ve been messing around with Esteve setting up an Amazon EC2 machine.

We set up a machine the other day, ssh’d into it, took a look around, and then shut it down a little later. Amazon just sent me a bill:

Greetings from Amazon Web Services,

This e-mail confirms that your latest billing statement is available on the AWS web site. Your account will be charged the following:

Total: $0.14

Please see the Account Activity area of the AWS web site for detailed account information.

Isn’t that cool?

It would certainly cost more than 14 cents to get your hands on your own (virtual) Linux box any other way.

I’ve been out talking to people about raising money for Fluidinfo.

Over the last 7 years I’ve read literally thousands of articles on talking to potential investors, pitching, raising money, angels, VCs, dilution, control, rounds, boards, strategies, valuations, burn rates, equity, etc. I’ve bought and read dozens of related books. I’m a regular reader of about a dozen VC blogs and the blogs of several entrepreneurs. I’ve swapped stories in person and learned lessons from probably a hundred other entrepreneurs. I was CTO of Eatoni Ergonomics, a startup that raised $5M in NYC, and I sat on the board for 4 years.

I like to analyze things, to sit around thinking, to generalize, to look for lessons, to find patterns, etc. So I reckon I have a fairly good idea of what creating a startup and raising money is about.

Some aspects of doing that are relatively formulaic. But others have significant variation.

For example, what should you put in a business plan? You can spend many months working on business plans. It’s hard work to write well and concisely. Then you show it to VC A and they tell you they’d also like to see X and Y and Z, that are not in your plan. So you put them in. You show it to VC B, and they tell you the plan is way too long! That you should take out P, Q, R and S. That leaves you with a wholly new-looking plan and when you show that to VC C, they’ll tell you it’s incoherent and doesn’t flow and look at you like you’re some kind of innocent child who doesn’t even know how to structure its thoughts. When you tell them you actually already know all that and that you agree, they’ll think you’re even weirder. And so it continues.

Thinking is changing on the business plan front, though. Some entrepreneurs and some investors have realized that creating or insisting on a business plan too early is probably a waste of time. Everyone knows the market numbers and the financial projections are probably rubbish. People expect the business and the plan to change, etc., etc.

When someone asks me for a business plan, I (politely) tell them I don’t have one or intend to write one. I tell them I’m looking for someone who wants to understand what I’m doing and fund it, without needing to see a formal written business plan. I suggest that if I reach the stage of looking for someone who wants the comfort of a better-thought-out plan that I will get back to them.

I think that’s a good change all round. You have to push back a little. A tiny engineering team focused on building a product probably shouldn’t stop, or be stopped, to write a business plan. I’m certainly not going to do that. I could spend that time writing code, working with people I’m paying to create more of a product, to get more online, to have more to point to, etc.

Elevator pitches

There’s definitely been a change with respect to business plans.

And now to the meat of this post, to a place where a similar change has yet to penetrate: the blind insistence on having an elevator pitch.

Almost universally, potential investors will want or expect an elevator pitch. Tons of VC sites will advise you that if you can’t describe your idea in a couple of sentences, it’s probably a non-starter. If you don’t have a compelling elevator pitch they wont talk to you, wont reply to email (even if you have been introduced), and they certainly wont read any materials.

Some even go so far as to tell you that without an elevator pitch you wont be able to communicate your ideas to your employees to motivate them! Uh, excuse me? Since when did the intelligent, driven, dig-in, curious, thoughtful, dedicated people who join startups acquire the attention span of gnats?

Listen. Some ideas can’t be summarized and/or grasped in a two-minute elevator ride. Sometimes you don’t even know yourself what the outcome will be. The history of science and innovation is full of examples. Imagine what the world would be like if, in order to get seed resources to push a new project along, all ideas had to be pre-vetted, each in 2 minutes, by a fairly general audience (I’m being polite again).

Entrepreneurs have to push back—where necessary—on the demand for an elevator pitch.

I’ve tried to put my round ideas into the square hole of an elevator pitch for long enough. I haven’t managed to do it and I don’t want to spend any more time trying.

Until tonight I’ve just been telling people I don’t have an elevator pitch, sorry. I’ve even told them (hi Nivi!) that instead of robotically insisting that I shape my ideas to their expectations that they try being more open minded about the process and try working on their expectations.

From now on, I’m going to give the following elevator pitch:

Here is a list of people. Each of them has had the curiousity, time, and patience to listen to my ideas for at least an hour. Ask them if I’m worth talking to further.

(See below for my list.)

If that’s not ok, then I agree that 1) if I reach the stage where I need to talk to people who really need an elevator pitch, and 2) you’re still interested, then I’ll try again to work on getting you what you need. Same goes for a business plan.

Up to this point I’ve tried to only talk to people who are willing to put the time in, to listen and think, to talk among themselves and draw their own conclusions. But I’ve still run into a bunch of people who wont do that. That’s ok, of course. I also know what it’s like to be busy.

Here’s my list. I’m very happy and very thankful to have recently spent at least an hour, sometimes much more, with each of the following:

Bradley Allen,
Art Bergman,
Jason Calacanis,
Dick Costolo,
Daniel Dennett.
Esther Dyson (now an investor),
Brady Forrest,
Eric Haseltine,
David Henkel-Wallace,
Jim Hollan,
Steve Hofmeyr,
Mark Jacobsen,
Vicente Lopez,
Roger Magoulas,
Jerry Michalski,
Nelson Minar,
Roger Moody,
Ted Nelson,
Tim O’Reilly,
Norm Packard,
Jennifer Pahlka,
Andrew Parker,
Scott Rafer,
Clay Shirky,
Reshma Sohoni,
Graham Spencer,
Stefan Tirtey,
Mark Tluszcz,
David Weinberger, and
Fred Wilson.

That’s my new elevator pitch.

If you buy it, let’s talk properly sometime soon. If you don’t, but you’re still curious, talk to some of those folks. Take your pick.

And if you don’t know any of those people, maybe you should be sending me your elevator pitch.